Kategoriarkiv: computer stuff

Books and lessons about ggplot2

Publicerat i computer stuff, data analysis, english av

I recently got an email from a person at Packt publishing, who suggested I write a book for them about ggplot2. My answer, which is perfectly true, is that I don’t have the time, nor the expertise to do that. What I didn’t say is that 1) a quick web search suggests that Packt doesn’t have the best reputation and 2) there are already two books about ggplot2 that I think covers the entire field: the indispensable ggplot2 book, written by Hadley Wickham, the author of the package, and the R Graphics Cookbok by Wincent Chang. There are too many decent but not great R books on the market already and there is no reason for me to spend time to create another one.

However, there are a few things I’d like to tell the novice, in general, about ggplot2:

1. ggplot2 is not necessarily superior to lattice or base graphics. It’s largely a matter of taste, you can make very nice plots with either plotting system and in some situations everybody will turn away from their favourite system and use another. For instance, a lot of built-in diagnostic plots come preprogrammed in base graphics. The great thing about ggplot2 is how it allows the user to think about plots as layers of mappings between variables and geometric objects. Base graphics and lattice are organised in different ways, which is not necessarily worse; it depends on the way you’re accustomed to thinking about statistical graphics.

2. There are two ways to start a plot in ggplot2: qplot( ) or ggplot( ). qplot is the quicker way and probably the one you should learn first. But don’t be afraid of the ggplot function! All it does is set up an empty plot and connect a data frame to it. After that you can add your layers and map your variables almost the same way you would do with qplot. After you’ve become comfortable with qplot, just try building plots with ggplot a few times, and you’ll see how similar it is.

3. The magic is not in plotting the data but in tidying and rearranging the data for plotting. Make sure to put all your labels, indicators and multiple series of data into the same data frame (most of the time: just cbind or merge them together), melt the data frame and pass it to ggplot2. If you want to layer predictions on top of your data, put output from your model in another data frame. It is perfectly possible, often advisable, to write functions that generate ggplot2 plots, but make sure to always create the data frame to be plotted first and then pass it on. I suggest not trying to create the mappings, that is x= and y= and the like, on the fly. There is always the risk of messing up the order of the vectors, and also, because ggplot2 uses metaprogramming techniques for the aesthetics, you might see unexpected behaviours when putting function calls into the mapping.

4. Worry about mapping variables and facetting first and then change the formatting. Because of how plots as well as settings in ggplot2 are objects that you can store and pass around, you can first create a raw version of the plot, and then just add (yes add, with the ”+” operator) the formatting options you want. So taken together, the workflow for making any ggplot2 plot goes something like this: 1) put your data frame in order; 2) set up a basic plot with the qplot or ggplot function; 3) add one extra geom at at time (optional if you make a simple plot with qplot, since qplot sets up the first geometry for you); 4) add the settings needed to make the plot look good.

Happy ggplotting!

Bracketing part of a dna sequence in Javascript

Publicerat i computer stuff, english av

Sometimes you just need a quick script to make life easier. This is an example of a small task: You have a dna sequence extracted from some bigger corpus, such as a reference genome sequence, and you know that there is something interesting going on 200 bp into the sequence. So you’ve downloaded a fasta file, and you want the computer to count 200 bases of flanking sequence and highlight the interesting thing for you. This problem arises naturally when designing primers, for example. You can use any scripting language you want, but if you want it to be used by a person who does not (yet) use command line based tools, if you’d like it to run on their computer that runs a different operating system than yours does, and if want to make a graphical user interface as quickly as possible — Javascript is actually an excellent weapon of choice.

Therefore, the other day, I wrote this little thing in Javascript. Mind you, it was ages since I last touched Javascript or html, and it’s certainly not a thing of beauty. But it does save time and I think I’ve avoided the most egregious errors. Everything is contained in the html page, so it’s actually a small bioinformatics script that runs in the browser.

Here is the Javascript part: a single procedure that extracts the parameters (the sequence and the number of flanking bases before and after), uses regular expressions to remove any fasta header, whitespaces and newlines, slices the resulting cleaned sequence up in three pieces, and outputs it with some extra numbers.

function bracketSequence (form) {
   var before = form.flank_before.value;
   var after = form.flank_after.value;
   var seq = form.sequence.value;

   // Find and remove fasta header
   fastaHeader = seq.match(/^>.*[\r\n|\n|\r]/, "");
   seq = seq.replace(/(^>.*(\r\n|\n|\r))/, "");

   // Remove whitespace and newlines
   seq = seq.replace(/(\r\n|\n|\r| )/gm, "");

   seqBefore = seq.slice(0, before);
   seqCore = seq.slice(before, seq.length - after);
   seqAfter = seq.slice(seq.length - after, seq.length);
   form.output.value = seqBefore + "[" + seqCore + "]" + seqAfter;

   form.fasta_header.value = fastaHeader;

   document.getElementById("core_length").innerHTML = seqCore.length;
   document.getElementById("before_length").innerHTML = seqBefore.length;
   document.getElementById("after_length").innerHTML = seqAfter.length;
}

I know, I know — the regular expressions look like emoticons that suffered through a serious accident. The fasta header expression ”^>.*[\r\n|\n|\r]/” matches the beginning of the file up to any linebreak character. The other expression ”(\r\n|\n|\r| )” just matches linebreaks and whitespace. This means the fasta header has to start with the ”>”; it cannot have any whitespace before. Other than whitespace, strange characters in the sequence should be preserved and counted.

The input and output uses a html form and a couple of named pieces of html (‘spans’). Here we put two textboxes to input the numbers, a big textarea for the sequence, and then a textarea, a textbox and some spans for the output. The onClick action of the button runs the procedure.

<form name="form" action="" method="get">

<p>Flanking bases before: <input type="text" name="flank_before"
value="" /></p>

<p>Flanking bases after: <input type="text" name="flank_after"
value="" /></p>

<p>Your sequence:</p>

<textarea name="sequence" rows="5" cols="80">
</textarea>

<p><input type="button" name="button" value="Go"
onClick="bracketSequence(this.form)" /></p>

<p>Output sequence:</p>

<textarea name="output" rows="5" cols="80">
</textarea>

<p>Fasta header: <input type="text" name="fasta_header" value="" /></p>

<p>Length of core sequence: <span id="core_length"></span></p>
<p>Length of flank before: <span id="before_length"></span></p>
<p>Length of flank after: <span id="after_length"></span></p>

</form>

Using R: Coloured sizeplot with ggplot2

Publicerat i computer stuff, data analysis, english av

Someone asked about this and I though the solution with ggplot2 was pretty neat. Imagine that you have a scatterplot with some points in the exact same coordinates, and to reduce overplotting you want to have the size of the dot indicating the number of data points that fall on it. At the same time you want to colour the points according to some categorical variable.

The sizeplot function in the plotrix package makes this type of scatterplot. However, it doesn’t do the colouring easily. I’m sure it’s quite possible with a better knowledge of base graphics, but I tend to prefer ggplot2. To construct the same type of plot we need to count the data points. For this, I use table( ), and then melt the contingency table and remove the zeroes.

library(ggplot2)
library(reshape2)
data <- data.frame(x=c(0, 0, 0, 0, 1, 1, 2, 2, 3, 3, 4, 4),
                   y=c(0, 0, 0, 3, 1, 1, 1, 2, 2, 1, 4, 4),
                   group=c(rep(1, 6), rep(2, 4), rep(3, 2)))
counts <- melt(table(data[1:2]))
colnames(counts) <- c(colnames(data)[1:2], "count")
counts <- subset(counts, count != 0)
sizeplot <- qplot(x=x, y=y, size=count, data=counts) + scale_size(range=c(5, 10))

scaleplot_1

This is the first sizeplot. (The original scale makes single points very tiny. Hence the custom scale for size. Play with the range values to taste!) To add colour, we merge the counts with the original data to get back the group information — and, in true ggplot2 fashion, map the group variable to colour.

counts.and.groups <- merge(counts, unique(data))
sizeplot.colour <- qplot(x=x, y=y, size=count,
                         colour=factor(group), data=counts.and.groups) +
                     scale_size(range=c(5, 10))

sizeplot_2

One thing that this simple script does not handle well is if points that should have different colour happen to overlap. (As it stands, this code will actually plot two points both the size of the total number of overlapping points in different colours on top of each other. That must be wrong in several ways.) However, I don’t know what would be the best behaviour in this instance. Maybe to count the number of overlaps separately and plot both points while adding some transparency to the points?

A slightly different introduction to R, part V: plotting and simulating linear models

Publicerat i computer stuff, data analysis, english av

In the last episode (which was quite some time ago) we looked into comparisons of means with linear models. This time, let’s visualise some linear models with ggplot2, and practice another useful R skill, namely how to simulate data from known models. While doing this, we’ll learn some more about the layered structure of a ggplot2 plot, and some useful thing about the lm function.

11. Using points, lines and error bars to show predictions from linear models

Return to the model of comb gnome mass at time zero. We’ve already plotted the coefficient estimates, but let us just look at them with the coef() function. Here the intercept term is the mean for green comb gnomes subjected to the control treatment. The ‘grouppink’ and ‘treatmentpixies’ coefficients are the mean differences of pink comb gnomes and comb gnomes exposed to pixies from this baseline condition. This way of assigning coefficients is called dummy coding and is the default in R.

model <- lm(mass0 ~ group + treatment, data)
coef(model)[1]

    (Intercept)       grouppink treatmentpixies 
      141.56771       -49.75414        23.52428

The estimate for a pink comb gnome with pixies is:

coef(model)[1] + coef(model)[2] + coef(model)[3]

There are alternative codings (”contrasts”) that you can use. A common one in Anova is to use the intercept as the grand mean and the coefficients as deviations from the mean. (So that the coefficients for different levels of the same factor sum to zero.) We can get this setting in R by changing the contrasts option, and then rerun the model. However, whether the coefficients are easily interpretable or not, they still lead to the same means, and we can always calculate the values of the combinations of levels that interest us.

Instead of typing in the formulas ourself as above, we can get predictions from the model with the predict( ) function. We need a data frame of the new values to predict, which in this case means one row for each combination of the levels of group and treatment. Since we have too levels each there are only for of them, but in general we can use the expand.grid( ) function to generate all possible factor levels. We’ll then get the predictions and their confidence intervals, and bundle everything together to one handy data frame.

levels <- expand.grid(group=c("green", "pink"), treatment=c("control", "pixies"))
predictions <- predict(model, levels, interval="confidence")
predicted.data <- cbind(levels, predictions)

  group treatment       fit       lwr      upr
1 green   control 141.56771 125.82527 157.3101
2  pink   control  91.81357  76.48329 107.1439
3 green    pixies 165.09199 149.34955 180.8344
4  pink    pixies 115.33785  98.93425 131.7414

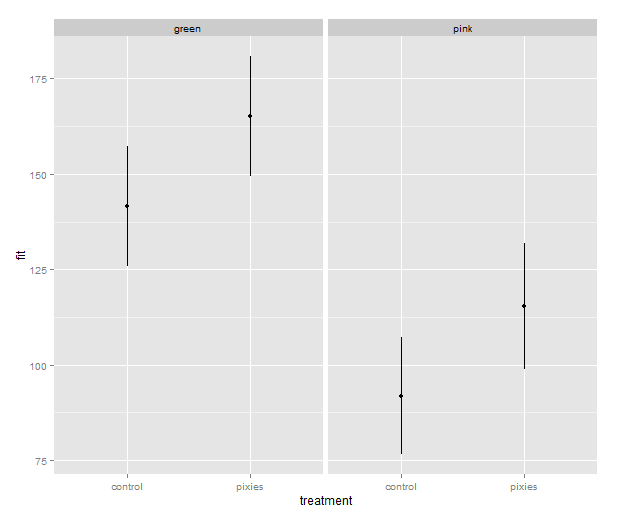
Now that we have these intervals in a data frame we can plot them just like we would any other values. Back in part II, we put several categorical variables into the same plot by colouring the points. Now, let’s introduce nice feature of ggplot2: making small multiples with faceting. qplot( ) takes facets argument which is a formula where the left hand side, before the tilde (‘~’), will be used to split the plot vertically, and the right hand side will split the plot horizontally. In this case, we split horizontally, each panel representing one level of the treatment variable. Also, we use a new geometry: pointrange, which draws a point with bars above and below it and is quite suitable for the intervals we’ve got.

qplot(x=treatment, facets=~group,
      y=fit, ymax=upr, ymin=lwr
      geom="pointrange", data=predicted.data)

model_lineranges

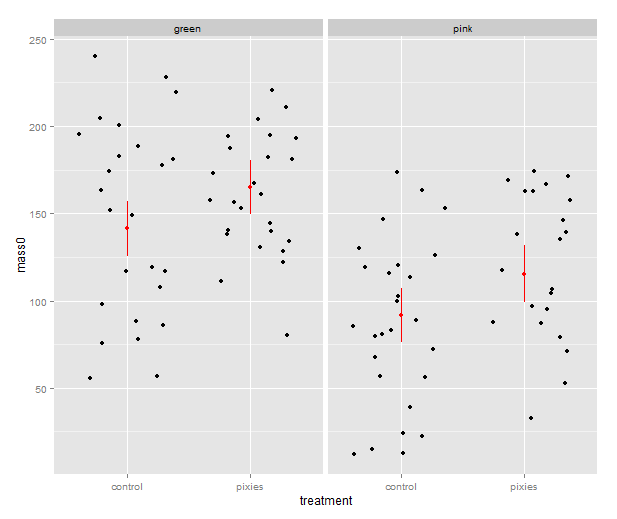
That’s good, but combining the predictions from the model and the actual data in the same plot would be nice. In ggplot2, every plot is an object that can be saved away to a variable. Then we can use the addition operator to add layers to the plot. Let’s make a jittered dotplot like the above and then add a layer with the pointrange geometry displaying confidence intervals. The scatter of the data points around the confidence intervals reminds us that there is quite a bit of residual variance. The coefficient of determination, as seen in the summary earlier, was about 0.25.

qplot(x=treatment, y=mass0, facets=~group, geom="jitter", data=data) +
    geom_pointrange(aes(y=fit, ymax=upr, ymin=lwr), colour="red", data=predicted.data)

model_jitter

In the above, we make use of ggplot2’s more advanced syntax for specifying plots. The addition operator adds layers. The first layer can be set up with qplot(), but the following layers are made with their respective functions. Mapping from variables to features of the plot, called aesthetics, have to be put inside the aes() function. This might look a bit weird in the beginning, but it has its internal logic — all this is described in Hadley Wickham’s ggplot2 book.

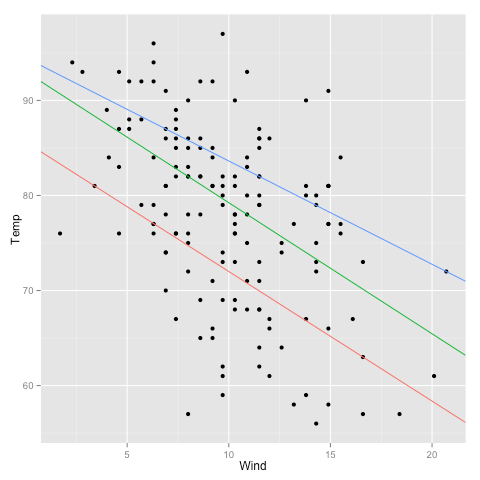
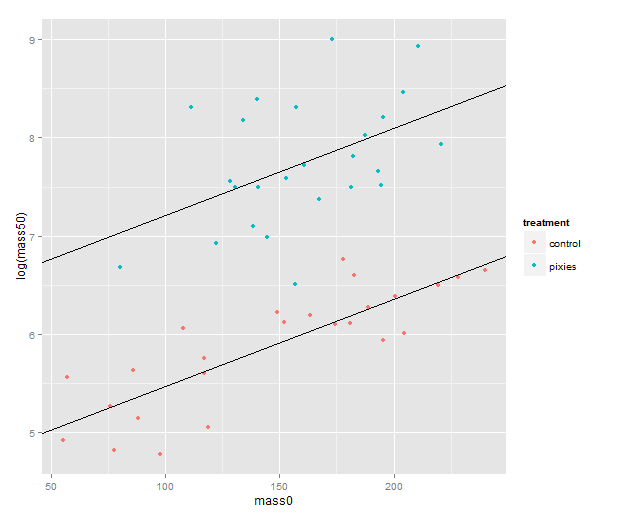
We should probably try a regression line as well. The abline geometry allows us to plot a line with given intercept and slope, i.e. the coefficients of a simple regression. Let us simplify a little and look at the mass at time zero and the log-transformed mass at time 50 in only the green group. We make a linear model that uses the same slope for both treatments and a treatment-specific intercept. (Exercise for the reader: look at the coefficients with coef( ) and verify that I’ve pulled out the intercepts and slope correctly.) Finally, we plot the points with qplot and add the lines one layer at the time.

green.data <- subset(data, group=="green")
model.green <- lm(log(mass50) ~ mass0 + treatment, green.data)
intercept.control <- coef(model.green)[1]
intercept.pixies <- coef(model.green)[1]+coef(model.green)[3]
qplot(x=mass0, y=log(mass50), colour=treatment, data=green.data) +
   geom_abline(intercept=intercept.pixies, slope=coef(model.green)[2]) +
   geom_abline(intercept=intercept.control, slope=coef(model.green)[2])

regression_lines

12. Using pseudorandom numbers for sanity checking

There is a short step from playing with regression functions that we’ve fitted, like we did above, to making up hypothetical regression functions and simulating data from them. This type of fake-data simulation is very useful to for testing how designs and estimation procedures behave and check things like the control of false positive rate and the power to accurately estimate a known model.

The model will be the simplest possible: a single categorical predictor with only two levels and normally distributed equal error variance, i.e. a t-test. There is a formula for the power of the t-test and an R function, power.t.test( ), that calculates it for us without the need for simulation. However, a nice thing about R is that we can pretty easily replace the t-test with more complex procedures. Any model fitting process that you can program in R can be bundled into a function and applied to pseudorandom simulated data. In the next episode we will go into how to make functions and apply them repeatedly.

Let us start out with a no effect model: 50 observations in two groups drawn from the same distribution. We use the mean and variance of the green control group. This first part just sets up the variables:

mu <- mean(subset(data, group=="green" & treatment=="control")$mass0)
sigma <- sd(subset(data, group=="green" & treatment=="control")$mass0)
treatment <- c(rep(1, 50), rep(0, 50))

The rnorm( ) function generates numbers from a normal distribution with specified mean and standard deviation. Apart from drawing numbers from it, R can of course pull out various table values, and it knows other distributions as well. Look at the documentation in ?distributions. Finally we perform a t-test. Most of the time, it should not show a significant effect, but sometimes it will.

sim.null <- rnorm(100, mu, sigma)
t.test(sim.null ~ treatment)$p.value

We can use the replicate( ) function to evaluate an expression multiple times. We put the simulation and t-test together into one expression, rinse and repeat. Finally, we check how many of the 1000 replicates gave a p-value below 0.05. Of course, it will be approximately 5% of them.

sim.p <- replicate(1000, t.test(rnorm(100, mu, sigma) ~ treatment)$p.value)
length(which(sim.p < 0.05))/1000

[1] 0.047

Let us add an effect! Say we’re interested in an effect that we expect to be approximately half the difference between the green and pink comb gnomes:

d <- mean(subset(data, group=="green" & treatment=="control")$mass0) -
     mean(subset(data, group=="pink" & treatment=="control")$mass0)
sim.p.effect <- replicate(1000, t.test(treatment * d/2 +
                                       rnorm(100, mu, sigma) ~ treatment)$p.value)
length(which(sim.p.effect < 0.05))/1000

[1] 0.737

We see that with 50 individuals in each group and this effect size we will detect a significant difference about 75% of the time. This is the power of the test. If you are able to find nice and trustworthy prior information about the kind of effect sizes and variances you expect to find in a study, design analysis allows you to calculate for instance how big a sample you need to have good power. Simulation can also give you an idea of how badly a statistical procedure will break if the assumptions don’t hold. We can try to simulate a situation where the variances of the two groups differs quite a bit.

sim.unequal <- replicate(1000, t.test(c(rnorm(50, mu, sigma),
                                        rnorm(50, mu, 2*sigma)) ~ treatment)$p.value)
length(which(sim.unequal < 0.05))/1000

[1] 0.043
sim.unequal.effect <- replicate(1000, t.test(c(rnorm(50, mu+d/2, sigma),
                                               rnorm(50, mu, 2*sigma)) ~ treatment)$p.value)
length(which(sim.unequal.effect < 0.05))/1000

[1] 0.373

In conclusion, the significance is still under control, but the power has dropped to about 40%. I hope that has given a small taste of how simulation can help with figuring out what is going on in our favourite statistical procedures. Have fun!

R intro seminars, take 2: some slides about data frames, linear models and statistical graphics

Publicerat i computer stuff, data analysis, english av

I am doing a second installment of the lunch seminars about data analysis with R for the members of the Wright lab. It’s pretty much the same material as before — data frames, linear models and some plots with ggplot2 — but I’ve sprinkled in some more exercises during the seminars. I’ve tried emphasising scripting a bit more than last time, and made a lot of use of RStudio. Going through this first part has taken four hours, but that includes each seminar a quick review of what we did last time and lots of questions. Next week we’ll get started on gene expression microarray data, and I’ll try introducing both limma and plyr.

(My previous introduction materials are posted here. Comments, suggestions and ideas about teaching R to biologists are always welcome!)

Using R: drawing several regression lines with ggplot2

Publicerat i computer stuff, data analysis av

Occasionally I find myself wanting to draw several regression lines on the same plot, and of course ggplot2 has convenient facilities for this. As usual, don’t expect anything profound from this post, just a quick tip!

There are several reasons we might end up with a table of  regression coefficients connecting two variables in different ways. For instance, see the previous post about ordinary and orthogonal regression lines, or as a commenter suggested: quantile regression. I’ve never used quantile regression myself, but another example might be plotting simulations from a regression or multiple regression lines for different combinations of predictors.

Let’s start with a couple of quantile regressions. Ordinary regression compares the mean difference in a response variable between different values of the predictors, while quantile regression models some chosen quantiles of the response variable. The rq function of Roger Koenker’s quantreg package does quantile regression. We extract the coefficient matrix and make a dataframe:

library(quantreg)
model.rq <- rq(Temp ~ Wind, airquality, tau=c(0.25, 0.5, 0.75))
quantile.regressions <- data.frame(t(coef(model.rq)))
colnames(quantile.regressions) <- c("intercept", "slope")
quantile.regressions$quantile <- rownames(quantile.regressions)
quantile.regressions

         intercept     slope  quantile
tau= 0.25 85.63636 -1.363636 tau= 0.25
tau= 0.50 93.03448 -1.379310 tau= 0.50
tau= 0.75 94.50000 -1.086957 tau= 0.75

The addition of the quantile column is optional if you don’t feel the need to colour the lines.

library(ggplot2)
scatterplot <- qplot(x=Wind, y=Temp, data=airquality)
scatterplot + geom_abline(aes(intercept=intercept, slope=slope,
  colour=quantile), data=quantile.regressions)

We use the fact that ggplot2 returns the plot as an object that we can play with and add the regression line layer, supplying not the raw data frame but the data frame of regression coefficients.

quantile_scatter

Slides from my R intro seminar

Publicerat i computer stuff, data analysis, english av

Here are my slides from a short introductory seminar on R (essentially going through part I of the R tutorial) last week. As magic lantern pictures go, they’re hideously ugly, but they were mostly there for future reference. Most of the seminar was spent showing RStudio. This Friday, we’ll practice some uses of qplot and make some linear models.

(I took out the Modern Major-General quote from the presentation, but you can enjoy him here instead. Don’t ask.)

Using R: reading tables that need a little cleaning

Publicerat i computer stuff av

Sometimes one needs to read tables that are a bit messy, so that read.table doesn’t immediately recognize the content as numerical. Maybe some weird characters are sprinkled in the table (ever been given a table with significance stars in otherwise numerical columns?). Some search and replace is needed. You can do this by hand, and I know this is a task for which many people would turn to a one-liner of perl or awk, but I like to do my scripting in R.

Again, this is in the ”trivial of you only think it out” category of problems. But it gives a starting point for more subtle changes to text files that one might have to do from time to time.

Assume the data look something like this (I made this up):

id;col1;col2
id1; 0,2;0.55*
id2; -,1;,23

Thankfully, R’s conversion from numbers to text is pretty good. It will understand, for instance, that both .5 and 0.5 are numbers. If the problem was just an odd decimal separator, like the Swedish decimal comma, we could just change the dec parameter to read.table. In the above, we have mixed decimal separators. Let’s start out by reading the table as character.

character.data <- read.table("some_data.csv", sep=";",
                   colClasses="character", header=T)
row.names(character.data) <- character.data[,1]
character.data <- character.data[,-1]

This also stores away the sample ids in row names, and removes the first column with the ids. This is optional, but for this example I assume that all columns should be numeric. If that is not the case, the code below can of course be restricted to the numeric columns, and the character (or factor) columns can be added later.

A data.frame is pretty much a list of vectors, so we use plyr to apply over the list and stringr to search and replace in the vectors. After removing characters that aren’t numbers, decimal separators, or the minus sign, we change the decimal separator, and convert the vector to numeric. Finally, we make the list a data.frame, and propagate the row names.

library(stringr)
library(plyr)

data <- data.frame(llply(character.data, function(x) {
  x <- str_replace_all(x, pattern="[^0-9\\.\\,-]", replacement="")
  x <- str_replace(x, pattern="\\,", replacement=".")
  return(as.numeric(x))
}))
row.names(data) <- row.names(character.data)

Using R: accessing PANTHER classifications

Publicerat i computer stuff, english, genetik av

Importing, subsetting, merging and exporting various text files with annotation (in the wide sense, i.e. anything that might help when interpreting your experiment) is not computation and it’s not biology either, but it’s housekeeping that needs to be done. Everyone has a weapon of choice for general-purpose scripting and mine is R. Yes, this is ”quite trivial if you only think it out”, but it still takes me some time. This script is a work in progress and could certainly be much cleaner and friendlier, but I’ll post it for the benefit of any other user that might google for this kind of thing.

Panther is a protein database with phylogenetic trees of proteins annotated with Gene Ontology terms and organised into pathways. (See the paper in the 2013 database issue of NAR.)  Right now, I’m after pathway classification of chicken proteins. The pathways are also available in some xml formats for systems biologists, but I’m going to use the classification table. It contains all UniProtKB proteins, so it should cover most known genes products.

Note, if you just want to check up on a few genes or a few pathways the Panther web interface seems pretty nice. If you’re after nice pathway diagrams, also check out the website and the SBML format. But for accessing classifications en masse, a treatment in R may be useful.

For this post, I’ve broken down the script into parts. If you want a function for the whole thing, see github.

First, download the classification data for your favourite organism from the Panther ftp.

  panther <- read.delim(filename, sep="\t", head=F,
                        stringsAsFactors=F)

  colnames(panther)[1] <- "gene.id"
  colnames(panther)[3:5] <- c("panther.id", "panther.family",
                            "panther.subfamily")
  colnames(panther)[6:8] <- c("go.mf", "go.bp", "go.cc")
  colnames(panther)[9:10] <- c("panther.ontology", "panther.pathway")

This is a tab separated text file. Since some fields at the end of lines may be left empty, we use read.delim instead of read.table. I add som column names that I think agrees reasonably well with the readme. The first is a  gene id string that contains mapping to Ensembl or Entrez ids, as well as the uniprot accession. It looks something like this:

CHICK|Gene=ENSGALG00000013995|UniProtKB=F1P447

CHICK|ENTREZ=378784|UniProtKB=Q75XU5

Of course, we want the ids as separate columns: stringr does regular expressions in a vectorised manner. str_match gets grouped matches into arrays. (Yes, it can be done with a single regexp, but I don’t take pleasure in that kind of thing.)

  panther$ensembl.id <- str_match(panther$gene, "Gene=(.*)\\|")[,2]
  panther$uniprot.id <- str_match(panther$gene, "UniProtKB=(.*)$")[,2]
  panther$entrez.id <- str_match(panther$gene, "ENTREZ=(.*)\\|")[,2]

The gene ontology fields are terms from each ontology, stringed together and separated by semicolons. This is not the best format for querying, so I’ll make a list of GO ids from each ontology:

  parse.go <- function(go.column) {
    go.list <- str_match_all(go.column, "GO:([0-9]*)")
    names(go.list) <- panther$gene.id.string
    go.list <- llply(go.list, function(x) {if (!is.null(dim(x))) x[,1]})
    return(go.list)
  }
  go.mf <- parse.go(panther$go.mf)
  go.bp <- parse.go(panther$go.bp)
  go.cc <- parse.go(panther$go.cc)

Finally, the pathway column. It says this in the readme:

***Example Pathway:
Inflammation mediated by chemokine and cytokine signaling pathway#Inflammation mediated by chemokine and cytokine signaling pathway#P00031>Integrin#Integrin#P00853;Integrin signalling pathway#Integrin signalling pathway#P00034>Integrin alpha#Integrin alpha#P00941

The format of the pathway information is: pathway_long_name#pathway_short_name#pathway_accession>
component_long_name#component_short_name#component_accession

Explanation of pathway accessions:
Gxxxxx Gene or RNA
Pxxxxx Protein
Sxxxxx small molecules
Uxxxxx others, such as ”unknown”, etc.

For now, I’d like to keep just the pathway id, which is the first id of each pathway entry. Again, there are often multiple entries for the same gene.

  pathway.list <- str_match_all(panther$panther.pathway,
                                "#([G,P,S,U][0-9]*)>")
  names(pathway.list) <- panther$gene.id.string
  pathway.list <- llply(pathway.list,
                        function(x) {if (!is.null(dim(x))) x[,2]})

We might want to have these additional descriptions (names of GO terms, name of pathway) later, but for now, I’ll be satisfied with the unique ids. Let’s package everything in a list, and slap a class attribute on it for good measure.

  panther.classification <- list(data=panther,
                                 go.mf=go.mf,
                                 go.bp=go.bp,
                                 go.cc=go.cc,
                                 panther.pathway=pathway.list)
  class(panther.classification) <- "panther.classification"

Now we can get the pathway ids associated with our favourite gene. Take for example GNB3 which has Uniprot id E1C9D6.

get.pathways <- function(panther, acc) {
  
  ix.uni <- which(panther$data$uniprot.id == acc)
  ix.ens <- which(panther$data$ensembl.id == acc)
  ix.ent <- which(panther$data$entrez.id == acc)
  
  if (length(ix.uni) > 0) {
    ix <- ix.uni
  } else if (length(ix.ens > 0)) {
    ix <- ix.ens
  } else if (length(ix.ent > 0)){
    ix <- ix.ent
  } 
  panther$panther.pathway[[ix]]
  
}
get.pathways(panther.classification, "E1C9D6")

I'll get back to this to maybe do something more useful with it.

More Haskell fun: the regress of a function

Publicerat i computer stuff, english av

I thought this was pretty funny. Let’s follow the development of one part of my toy bootstrap script. (You have to keep in mind that I’m playing around with functional programming for the first time and that I’m completely utterly horrible at this!) So far, using pseudorandom draws with replacement from a list of data, my script will produce bootstrap replicates of that list. This is the part that, after the random draws have been partitioned into lists of sufficient length goes on to pull out the right elements of the data. The first iteration (heh) goes like this with explicit recursion:

applyShuffle x shuffle =
  if shuffle == [] then
    []
  else
    [x !! head shuffle] ++ applyShuffle x (tail shuffle)

applyShuffleOrder x shuffleOrder =
  if shuffleOrder == [] then
    []
  else
    [applyShuffle x (head shuffleOrder)] ++
       applyShuffleOrder x (tail shuffleOrder)

So, a ”shuffle” in the above is a list of indices of elements of data that form a bootstrap replicate. A ”shuffle order” is a list of such lists. Next step, why not try some pattern matching? Also, the (x:xs) notation for lists makes it look a little more Haskell-y:

applyShuffle x [] = []
applyShuffle x (index:indices) =
    [x !! index] ++ applyShuffle x indices

applyShuffleOrder x [] = []
applyShuffleOrder x (shuffle:shuffles) =
    [applyShuffle x shuffle] ++
        applyShuffleOrder x shuffles

Enter the map function! Map really just applies a function recursively to a list. (For friends of R: it’s like llply or lapply.) It’s still recursion, but it kind of reads like what I would say if I was to tell somebody what the function does: ”map the applyShuffle function to the shuffles we’ve already generated”. This is the second function again, but with map:

applyShuffleOrder x shuffles =
  map f shuffles
  where f = applyShuffle x

At this point you might realise that the functions can be easily combined into something much shorter. That is, you dear reader might have realised that before, but for me it came at this point. I also decided to stop talking about shuffle orders, and simply call them shuffles. At the end, this is all that remains of the above functions.

applyShuffles x shuffles =
  map applyShuffle shuffles
    where applyShuffle = map (x !!)