Ah, the barplot. Loved by some, hated by some, the first graph you’re likely to make in your favourite office spreadsheet software, but a rather tricky one to pull off in R. Or, that depends. If you just need a barplot that displays the value of each data point as a bar — which is one situation where I like a good barplot — the barplot( ) function does just that:

some.data <- rnorm(10, 4, 1.5)
names(some.data) <- 1:10
barplot(some.data)

Done? Not really. The barplot (I know some people might not use the word plot for this type of diagram, but I will) one typically sees from a spreadsheet program has some gilding: it’s easy to get several variables (”series”) of data in the same plot, and often you’d like to see error bars. All this is very possible in R, either with base graphics, lattice or ggplot2, but it requires a little more work. As usual when it gets a bit more fancy, I prefer ggplot2 over the alternatives. Once upon a time when I started with ggplot2, I tried googling for this, and lots of people have answered this question. I was still confused, though. So, if you’re a new user and reading this, please bear with me and I’ll try to demonstrate what all the steps are good for. Whether it’s a good statistical graph or not, the barplot is actually a nice example of ggplot2 in action and will demonstrate some R principles.

Let us take an example: Say that we start with a pretty typical small dataset with two variables that we’ve measured in four groups. Now we’d like a barplot of the group means and error bars for the means.

0. Start a script

Making the plot will take more than a couple of lines, so it’s a good idea to put everything in a script. Below I will split the script into chunks, but the whole thing is on github. We make a new R file and load ggplot2, plyr and reshape2, the packages we will need:

library(ggplot2)
library(plyr)
library(reshape2)

1. Simulate some data

In the case of real barplot this is where you load your data. You will probably have it in a text file that you read with the read.table( ) family of functions or RStudios Import dataset button (which makes the read.table call for you; if you don’t feel like late nights hunched over the read.table manual page, I recommend it). Simulating data might look something like this:

n <- 10
group <- rep(1:4, n)
mass.means <- c(10, 20, 15, 30)
mass.sigma <- 4
score.means <- c(5, 5, 7, 4)
score.sigma <- 3
mass <- as.vector(model.matrix(~0+factor(group)) %*% mass.means) +
  rnorm(n*4, 0, mass.sigma)
score <- as.vector(model.matrix(~0+factor(group)) %*% score.means) +
  rnorm(n*4, 0, score.sigma)
data <- data.frame(id = 1:(n*4), group, mass, score)

This code is not the tersest possible, but still a bit tricky to read. If you only care about the barplot, skip over this part. We define the number of individuals per group (10), create a predictor variable (group), set the true mean and standard deviation of each variable in each group and generate values from them. The values are drawn from a normal distribution with the given mean and standard deviation. The model.matrix( ) function returns a design matrix, what is usually called X in a linear model. The %*% operator is R’s way of denoting matrix multiplication — to match the correct mean with the predictor, we multiply the design matrix by the vector of means. Now that we’ve got a data frame, we pretend that we don’t know the actual values set above.

  id group       mass    score
1  1     1  4.2367813 5.492707
2  2     2 16.4357254 1.019964
3  3     3 19.2491831 6.936894
4  4     4 23.4757636 3.845321
5  5     1  0.9533737 1.852927
6  6     2 19.9142350 5.567024

2. Calculate means

The secret to a good plot in ggplot2 is often to start by rearranging the data. Once the data is in the right format, mapping the columns of the data frame to the right element of the plot is the easy part. In this case, what we want to plot is not the actual data points, but a function of them — the group means. We could of course subset the data eight times (four groups times two variables), but thankfully, plyr can do that for us. Look at this piece of code:

melted <- melt(data, id.vars=c("id", "group"))
means <- ddply(melted, c("group", "variable"), summarise,
               mean=mean(value))

First we use reshape2 to melt the data frame from tabular form to long form. The concept is best understood by comparing the output and input of melt( ). Compare the rows above to these rows, which are from the melted data frame:

   id group variable      value
1   1     1     mass  4.2367813
2   2     2     mass 16.4357254
3   3     3     mass 19.2491831
4   4     4     mass 23.4757636

We’ve gone from storing two values per row (mass and score) to storing one value (mass or score), keeping the identifying variables (id and group) in each row. This might seem tricky (or utterly obvious if you’ve studied database design), but you’ll soon get used to it. Trust me, if you do, it will prove useful!

The second row uses ddply (”apply from data frame to data frame”) to split up the melted data by all combinations of group and variable and calculate a function of the value, in this case the mean. The summarise function creates a new data frame from an old; the arguments are the new columns to be calculated. That is, it does exactly what it says, summarises a data frame. If you’re curious, try using it directly. It’s not very useful on its own, but very good in ddply calls.

3. Barplot of the means

Time to call on ggplot2! One has a choice between using qplot( ) or ggplot( ) to build up a plot, but qplot is the easier. We map the mean to y, the group indicator to x and the variable to the fill of the bar. The bar geometry defaults to counting values to make a histogram, so we need to tell use the y values provided. That’s what setting stat= to ”identity” is good for. To make the bars stand grouped next to each other instead of stacking, we tell set position=.

means.barplot <- qplot(x=group, y=mean, fill=variable,
                       data=means, geom="bar", stat="identity",
                       position="dodge")

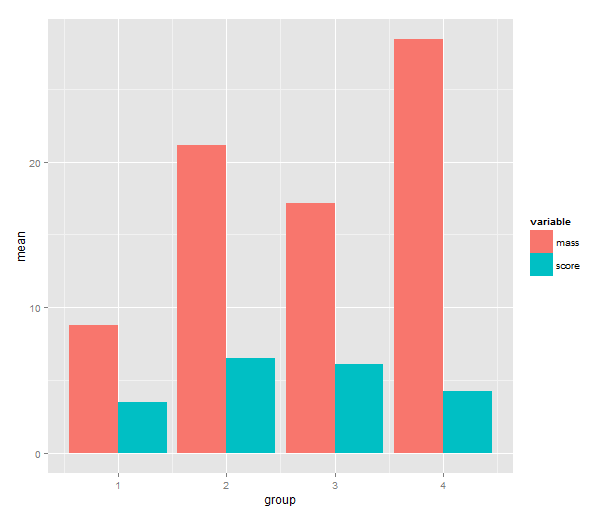
4. Standard error of the mean

Some people can argue for hours about error bars. In some cases you will want other types of error bars. Maybe the inferences come from a hierarchical model where the standard errors are partially pooled. Maybe you’re dealing with some type of generalised linear model or a model made with transformed data. See my R tutorial for a simple example with anova. The point is that from the perspective of ggplot2 input to the error bars is data, just like anything else, and we can use the full arsenal of R tools to create them.

means.sem <- ddply(melted, c("group", "variable"), summarise,
                   mean=mean(value), sem=sd(value)/sqrt(length(value)))
means.sem <- transform(means.sem, lower=mean-sem, upper=mean+sem)

First, we add a standard error calculation to the ddply call. The transform function adds colums to a data frame; we use it to calculate the upper and lower limit to the error bars (+/- 1 SEM). Then back to ggplot2! We add a geom_errorbar layer with the addition operator. This reveals some of the underlying non-qplot syntax of ggplot2. The mappings are wrapped in the aes( ), aesthetics, function and the other settings to the layer are regular arguments. The data argument is the data frame with interval limits that we made above. The only part of this I don’t like is the position_dodge call. What it does is nudge the error bars to the side so that they line up with the bars. If you know a better way to get this behaviour without setting a constant, please write me a comment!

means.barplot + geom_errorbar(aes(ymax=upper,
                                  ymin=lower),
                              position=position_dodge(0.9),
                              data=means.sem)

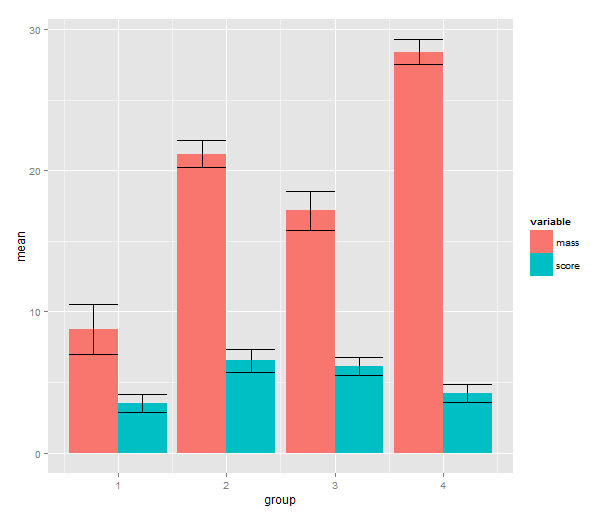
Does this seem like a lot of code? If we look at the actual script and disregard the data simulation part, I don’t think it’s actually that much. And if you make this type of barplot often, you can package this up into a function.