Now, after reading in data, making plots and organising commands with scripts and Sweave, we’re ready to do some numerical data analysis. If you’re following this introduction, you’ve probably been waiting for this moment, but I really think it’s a good idea to start with graphics and scripting before statistical calculations.
We’ll use the silly comb gnome dataset again. If you saved an Rdata file in part II, you can load it with
load("comb_gnome_data.Rdata")
If not, you can run this. Remind yourself what the changes to the melted data mean:
data <- read.csv("comb_gnome_data.csv")
library(reshape2)
melted <- melt(data, id.vars=c("id", "group", "treatment"))
melted$time <- 0
melted$time[which(melted$variable=="mass10"] <- 10
melted$time[which(melted$variable=="mass25")] <- 25
melted$time[which(melted$variable=="mass50")] <- 50
melted$id <- factor(melted$id)
We’ve already looked at some plots and figured out that there looks to be substantial differences in mass between the green and pink groups, and the control versus treatment. Let’s try to substantiate that with some statistics.
9. Mean and covariance
Just like anything in R, statistical tools are functions. Some of them come in special packages, but base R can do a lot of stuff out of the box.
Comparsion of two means: We’ve already gotten means from the mean() function and from summary(). Variance and standard deviation are calculated with var() and sd() respectively. Comparing the means betweeen two groups with a t-test or a Wilcoxon-Mann-Whitney test is done with t.test() and wilcox.test(). The functions have the word test in their names, but t-test gives not only the test statistics and p-values, but also estimates and confidence intervals. The parameters are two vectors of values of each group (i.e. a column from the subset of a data frame), and some options.
Looking back at this plot, I guess no-one is surprised by a difference in birthweigh between pink and green comb gnomes:
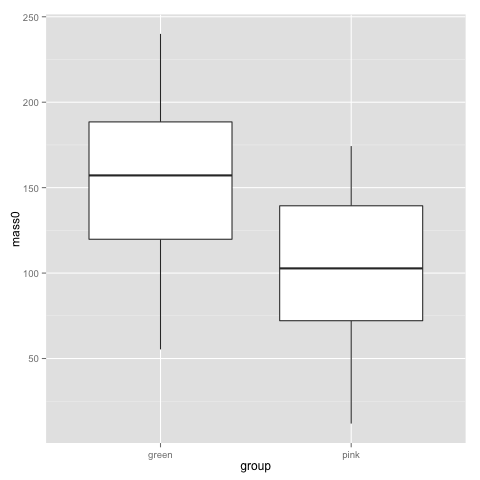
t.test(subset(data, group=="pink")$mass0, subset(data, group=="green")$mass0)
Welch Two Sample t-test
data: subset(data, group == "pink")$mass0 and subset(data, group == "green")$mass0
t = -5.397, df = 96.821, p-value = 4.814e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-69.69294 -32.21577
sample estimates:
mean of x mean of y
102.3755 153.3298
That is, we feed in two pieces of data (two vectors, really, which is what you get pulling out a column from a data frame). The above is the typical situation when you have all data points in one column and a group indicator in another. Hence you begin by subsetting the data frame to get the right rows, and pull out the right columns with the $. t.test also does paired tests, with the additional parameter paired=T.
wilcox.test(subset(data, group=="pink")$mass50, subset(data, group=="green")$mass50)
Wilcoxon rank sum test with continuity correction
data: subset(data, group == "pink")$mass50 and subset(data, group == "green")$mass50
W = 605, p-value = 1.454e-05
alternative hypothesis: true location shift is not equal to 0
Recalling histograms for the comb gnome weights, the use of the Wilcoxon-Mann-Whitney for masses at tim 50 and a t-test for the masses at birth (t=0) probably makes sense. However, we probably want to make use of all the time points together rather than doing a test for each time point, and we also want to deal with both the colour and the treatment at the same time.
Before we get there, let’s look at correlation:
cor(data$mass10, data$mass25)
cor(data$mass0, data$mass50, method="spearman")
cor.test(data$mass10, data$mass25)
The cor() function gives you correlation coefficients, both Pearson, Spearman and Kendall. If you want the covariance, cov() is the function for that. cor.test() does associated tests and confidence intervals. One thing to keep in mind is missing values. This data set is complete, but try this:
some.missing <- data$mass0
some.missing[c(10, 20, 30, 40:50)] <- NA
cor(some.missing, data$mass25)
cor(some.missing, data$mass10, use="pairwise")
The use parameter decides what values R should include. The default is all, but we can choose pairwise complete observations instead.
If you have a big table of variables that you’d like to correlate with each other, the cor() function works for them as well. (Not cor.test(), though. However, the function can be applied across the rows of a data frame. We’ll return to that.)
10. A couple of simple linear models
Honestly, most of the statistics in biology is simply linear models fit with least squares and tested with a normal error model. A linear model looks like this
yi = b0 + b1x1i + b2x2i + … bnxni + ei
where y is the response variable, the xs are predictors, i is an index over the data points, and ei are the errors. The error is the only part of the equations that is a random variable. b0, …, bn are the coefficients — your main result, showing how the mean difference in the response variable between data points with different values of the predictors. The coefficients are fit by least squares, and by estimating the variance of the error term, we can get some idea of the uncertainty in the coefficients.
Regression coefficients can be interpreted as predictions about future values or sometimes even as causal claims (depending on other assumptions), but basically, they describe differences in mean values.
This is not a text on linear regression — there are many of those; may I suggest the books by Faraway or Gelman and Hill — suffice to say that as long as the errors are independent and have equal variance, least squares is the best unbiased estimate. If we also assume that the errors are normally distributed, the least squares is also the maximum likelihood estimate. (And it’s essentially the same as a Bayesian version of the linear model with vague priors, just for the record.)
In R, the lm() function handles linear models. The model is entered as a formula of the type response ~ predictor + predictor * interacting predictors. The error is implicit, and assumed to be normally distributed.
model <- lm(mass0 ~ group + treatment, data=data)
summary(model)
Call:
lm(formula = mass0 ~ group + treatment, data = data)
Residuals:
Min 1Q Median 3Q Max
-86.220 -32.366 -2.847 35.445 98.417
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 141.568 7.931 17.850 < 2e-16 ***
grouppink -49.754 9.193 -5.412 4.57e-07 ***
treatmentpixies 23.524 9.204 2.556 0.0122 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 45.67 on 96 degrees of freedom
Multiple R-squared: 0.28, Adjusted R-squared: 0.265
F-statistic: 18.67 on 2 and 96 DF, p-value: 1.418e-07
The summary gives the coefficients, their standard errors, the p-value of a t-test of the regression coefficient, and R squared for the model. Factors are encoded as dummy variables, and R has picked the green group and the control treatment as baseline so the coefficient ”grouppink” describes how the mean of the pink group differs from the green. Here are the corresponding confidence intervals:
confint(model)
2.5 % 97.5 %
(Intercept) 125.825271 157.31015
grouppink -68.001759 -31.50652
treatmentpixies 5.254271 41.79428
(These confidence intervals are not adjusted to control the family-wise error rate, though.) With only two factors, the above table is not that hard to read, but let’s show a graphical summary. Jared Lander’s coefplot gives us a summary of the coefficients:
install.packages("coefplot") ##only the first time
library(coefplot)
coefplot(model)

The bars are 2 standard deviations. This kind of plot gives us a quick look at the coefficients, and whether they are far from zero (and therefore statistically significant). It is probably more useful for models with many coefficients.
There is a bunch of diagnostic plots that you can make to check for gross violations of the above assumptions of the linear model. Two useful ones are the normal quantile-quantile plot of residuals, and the residuals versus fitted scatterplot:
library(ggplot2)
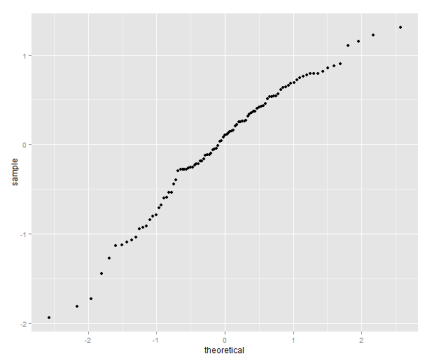
qplot(sample=residuals(model), stat="qq")
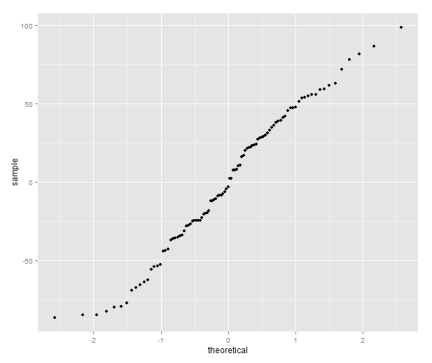
The quantile plot compares the distribution of the residual to the quantiles of a normal distribution — if the residuals are normally distributed it will be a straight line.
qplot(fitted(model), residuals(model))

Variance should be roughly equal fitted values, and there should not be obvious patterns in the data.
If these plots look terrible, a common approach is to try to find a transformation of the data that allows the linear model to be used anyway. For instance, it often helps to take the logarithm of the response variable. Why is that so useful? Well, with some algebraic magic:
log(yi) = b0 + b1x1i + b2x2i + … + bnxni + ei, and as long as no y:s are zero,
yi = exp(b0) * exp(b1x1i) * exp(b2x2i) * .. * exp(bnxni) * exp(ei)
We have gone from a linear model to a model where the b:s and x:es multiplied together. For some types of data, this will stabilise the variance of the errors, and make the distribution closer to a normal distribution. It’s by no means a panacea, but in the comb gnome case, I hope the plots we made in part II have already convinced you that an exponential function might be involved.
Let’s look at a model where these plots look truly terrible: the weight at time 50.
model.50 <- lm(mass50 ~ group + treatment, data=data)
qplot(sample=residuals(model.50), stat="qq")
qplot(fitted(model.50), residuals(model.50))


Let’s try the log transform:
model.log.50 <- lm(log(mass50) ~ group + treatment, data=data)
qplot(sample=residuals(model.log.50), stat="qq")
qplot(fitted(model.log.50), residuals(model.log.50))
coefplot(model.log.50)


In both the above models both predictors are categorical. When dealing with categorical predictors, you might prefer the analysis of variance formalism. Anova is the same kind of linear model as regression (but sometimes parameterised slightly differently), followed by F-tests to check whether each predictor explains a significant amount of the variance in the response variable. In all the above models, the categorical variables only have two levels each, so interpretation is easy by just looking a coefficients. When you get to bigger models with lots of levels, F-tests let you test the effect of a ‘batch’ of coefficients corresponding to a variable. To see the (type II, meaning that we test each variable against the model including all other variables) Anova table for a linear model in R, do this:
comb.gnome.anova <- aov(log(mass50) ~ group + treatment, data=data)
drop1(comb.gnome.anova)
Single term deletions
Model:
log(mass50) ~ group + treatment
Df Sum of Sq RSS AIC F value Pr(>F)
<none> 47.005 -67.742
group 1 30.192 77.197 -20.627 61.662 5.821e-12 ***
treatment 1 90.759 137.764 36.712 185.361 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1